String Searching
Authors: Benjamin Qi, Siyong Huang, Dustin Miao
Knuth-Morris-Pratt and Z Algorithms (and a few more related topics).
Prerequisites
| Resources | ||||
|---|---|---|---|---|
| CPC | String Matching, KMP, Tries | |||
| CP2 | ||||
Single String
A Note on Notation:
For a string :
- denotes the size of string
- denotes the character at index starting from
- denotes the substring beginning at index and ending at index
- is equivalent to , represents the prefix ending at
- is equivalent to , represents the suffix beginning of .
- denotes concactinating to the end of . Note that this implies that addition is non-commutative.
Knuth-Morris-Pratt Algorithm
| Resources | ||||
|---|---|---|---|---|
| cp-algo | ||||
| PAPS | ||||
| GFG | ||||
| TC | ||||
Define an array of size such that is equal to the length of the longest nontrivial suffix of the prefix ending at position the coincides with a prefix of the entire string. Formally,
In other words, for a given index , we would like to compute the length of the longest substring that ends at , such that this string also happens to be a prefix of the entire string. One such string that satisfies this criteria is the prefix ending at ; we will be disregarding this solution for obvious reasons.
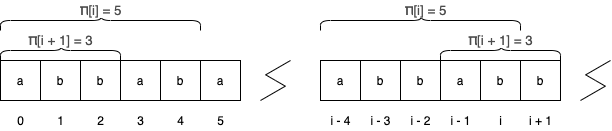
For instance, for , , and the prefix function of is . In the second example, because the prefix of length ( is equivalent to the substring of length that ends at index . In the same way, because the prefix of length () is equal to the substring of length that ends at index . For both of these samples, there is no longer substring that satisfies these criterias.
The purpose of the KMP algorithm is to efficiently compute the array in linear time. Suppose we have already computed the array for indices , and need to compute the value for index .
Firstly, note that between and , can be at most one greater. This occurs when .
In the example above, , meaning that a the suffix of length is equivalent to a prefix of length of the entire string. It follows that if the character at position of the string is equal to the character at position , then the match is simply extended by a single character. Thus, .
In the general case, however, this is not necessarily true. That is to say, . Thus, we need to find the largest index such that the prefix property holds (ie ). For such a length , we repeat the procedure in the first example by comparing characters at indicies and : if the two are equal, then we can conclude our search and assign , and otherwise, we find the next smallest and repeat. Indeed, notice that the first example is simply the case where begins as .
In the second example above, we let .
The only thing that remains is to be able to efficiently find all the that we might possibly need. To recap, if the position we're currently at is , to handle transitions we need to find the largest index that satisfies the prefix property . Since , this value is simply , a value that has already been computed. All that remains is to handle the case where . If , , otherwise .
C++
vector<int> pi(const string &s) {int n = (int)s.size();vector<int> pi_s(n);for (int i = 1, j = 0; i < n; i++) {while (j > 0 && s[j] != s[i]) { j = pi_s[j - 1]; }if (s[i] == s[j]) { j++; }pi_s[i] = j;}return pi_s;}
Python
from typing import Listdef pi(s: str) -> List[int]:n = len(s)pi_s = [0] * nj = 0for i in range(1, n):while j > 0 and s[j] != s[i]:j = pi_s[j - 1]if s[i] == s[j]:j += 1pi_s[i] = jreturn pi_s
Claim: The KMP algorithm runs in for computing the array on a string of length .
Proof: Note that doesn't actually change through multiple iterations. This is because on iteration , we assign . However, in the previous iteration, we assign to be . Furthermore, note that is always non-negative. In each iteration of , is only increased by at most in the if statement. Since remains non-negative and is only increased a constant amount per iteration, it follows that can only decrease by at most times through all iterations of . Since the inner loop is completely governed by , the overall complexity amortizes to .
Problems
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| CSES | Very Easy | Show TagsKMP, Z | |||
| POI | Easy | Show TagsKMP, Strings | |||
| Baltic OI | Normal | Show TagsKMP, Strings | |||
| Old Gold | Hard | Show TagsKMP, Strings | |||
| POI | Hard | Show TagsKMP, Strings | |||
| CEOI | Hard | Show TagsKMP | |||
| POI | Very Hard | Show TagsKMP | |||
| POI | Very Hard | Show TagsKMP |
Z Algorithm
The Z-Algorithm is another linear time string comparison algorithm like KMP, but instead finds the longest common prefix of a string and all of its suffixes.
| Resources | ||||
|---|---|---|---|---|
| cp-algo | ||||
| CPH | ||||
| CF | ||||
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| YS | Very Easy | Show TagsZ | |||
| CSES | Very Easy | Show TagsKMP, Z | |||
| CF | Normal | Show TagsDP, Strings | |||
| CF | Normal | Show TagsZ | |||
| CF | Hard |
Palindromes
Manacher
Focus Problem – try your best to solve this problem before continuing!
Manacher's Algorithm functions similarly to the Z-Algorithm. It determines the longest palindrome centered at each character.
| Resources | ||||
|---|---|---|---|---|
| HR | ||||
| CF | shorter code | |||
| cp-algo | ||||
Don't Forget!
If s[l, r] is a palindrome, then s[l+1, r-1] is as well.
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| CF | Normal | Show TagsStrings | |||
| CF | Normal | Show TagsStrings | |||
| CF | Hard | Show TagsPrefix Sums, Strings |
Palindromic Tree
A Palindromic Tree is a tree-like data structure that behaves similarly to KMP. Unlike KMP, in which the only empty state is , the Palindromic Tree has two empty states: length , and length . This is because appending a character to a palindrome increases the length by , meaning a single character palindrome must have been created from a palindrome of length
| Resources | ||||
|---|---|---|---|---|
| CF | ||||
| adilet.org | ||||
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| APIO | Easy | ||||
| CF | Hard | Show TagsPrefix Sums, Strings | |||
| DMOJ | Very Hard |
Multiple Strings
Tries
A trie is a tree-like data structure that stores strings. Each node is a string, and each edge is a character. The root is the empty string, and every node is represented by the characters along the path from the root to that node. This means that every prefix of a string is an ancestor of that string's node.
| Resources | ||||
|---|---|---|---|---|
| CPH | ||||
| CF | ||||
| PAPS | ||||
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| COCI | Very Easy | Show TagsDFS, Strings, Trie | |||
| IOI | Very Easy | Show TagsDFS, Strings, Trie | |||
| CSES | Very Easy | Show TagsDP, Strings | |||
| YS | Easy | Show TagsGreedy, Trie | |||
| Gold | Normal | Show TagsStrings, Trie | |||
| CF | Normal | Show TagsStrings, Trie | |||
| COCI | Normal | Show TagsTrie | |||
| AC | Normal | ||||
| CF | Normal | Show TagsSmall-to-large-merging, Tree, Trie | |||
| CF | Normal | Show TagsBitmasks, Tree, Trie | |||
| IZhO | Hard | Show TagsGreedy, Trie | |||
| JOI | Hard | Show TagsBIT, Trie | |||
| CF | Hard | Show TagsTree, Trie |
Aho-Corasick
Aho-Corasick is the combination of trie and KMP. It is essentially a trie with KMP's "fail" array.
Warning!
Build the entire trie first, and then run a BFS to construct the fail array.
| Resources | ||||
|---|---|---|---|---|
| cp-algo | ||||
| CF | ||||
| GFG | ||||
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| CF | Easy | Show TagsStrings | |||
| Gold | Normal | Show TagsStrings | |||
| CF | Normal | Show TagsStrings |
This section is not complete.
1731 Word Combinations -> trie
1732 Finding Borders -> string search
1733 Finding Periods -> string search
1110 Minimal Rotation -> string search
1111 Longest Palindrome -> string search
1112 Required Substring -> string search
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!